A matematikatanítás változásai...

…a XVI. századtól napjainkig. Köves Gabriella írása
A tanulmány bemutatja az első és második osztályos matematika tankönyvekben mindazokat a változásokat, amelyek a számfogalom alakítását érintették.
A történeti áttekintés világosan kimutatja az iskolák államosításával bekövetkezett matematika módszertani kutatás, beválási vizsgálat nélkül bevezetett metodikai váltást; amely napjainkig meghatározta a tananyagbeosztást. Útmutatást adhat az elkövetkező évek számfogalom-alakítási koncepciójának kidolgozásához, a jelenlegi kerettanterv adta lehetőségek alapján. A változtatást különösen indokolják a teljesítményvizsgálatokon nyújtott egyre romló eredmények.
A tematikában bekövetkezett változások
Az elemi szintű matematika tanítása egységes abban, hogy az első években a leghangsúlyosabban a számfogalmat kívánja kialakítani, a számkör fokozatos bővítésével, a fejszámolás és az írásbeli számolás megtanításával a természetes számok halmazán.
Az első magyar nyelvű számtankönyvek (1557–1777) [2.; 18.; 25–27.; 34.] mindjárt a könyvek elején egy lépésben bevezették a tanítani kívánt számkört (N-ben). Ebben az időszakban a szám- és műveletfogalom alakítását még teljes egészében különválasztották. Az I-II. Ratio Educationis tankönyvei már meghatározott korosztály számára készültek, ami indítéka lehetett a számkör fokozatos bevezetésének.
Amint erőteljesebben törekedtek az érthetőségre, a szemléltetésre, a fejszámolás tanítására, terjedni kezdett Friedrich Gottlieb von Busse (1756–1835) módszere. Számképein megjelenik egy-egy számhoz kapcsolható összeadás, szorzás. A XIX. század végére Busse [9.] hatására Magyarországon is elterjedt a szám- és műveletfogalom összekapcsolása.
A XIX-XX. század fordulójától a múlt század közepéig a tantervekből és a vezérkönyvekből tudni lehet, hogy első osztályban 20-ig vagy 30-ig bővítették a számkört. Minden számkörben elvégezték a négy alapműveletet.
E tekintetben változást hozott az iskolarendszer átformálásának időszaka (1947–), amikor az első osztályban 100-as számkörben számoltak. Három évvel később az Általános tankönyvben már csak helyiérték-átlépés nélkül végzik az összeadást és a kivonást 100-as számkörben, de a 20-as számkörben elvégezhető szorzást, osztást is bevezeti a Varga-tankönyv [33.]. Ebben az időszakban Varga próbálja visszahozni a XIX-XX. század fordulóján már bevett gyakorlatot, a szám- és műveletfogalom együttes fejlesztését, de nem talál követőkre. 1963-tól a Csáki-féle [11–12.] tankönyvekben a 20-as számkörben már csak az összeadás és kivonás marad meg, a szorzás-osztás kikerül a tananyagból, ami már valóságos tetemes tananyagcsökkenést jelent. A későbbi tankönyvek teljesen átvették Csáki koncepcióját.
A 2. osztályban is más-más módszertannal jelenik meg a számkör bővítése, a négy alapművelet begyakoroltatása, a műveletfogalom alakítása. A XX. század első felében a szám- és műveletfogalom alakítását párhuzamosan végezték, de a számkörbővítés lépéseiben, egy-egy számkör feldolgozásának menetében voltak különbségek. Császár [17.], Szirmai [37.], Schultz [35.] és Beke [6.] tankönyveiben látszik, hogy igyekeztek megtalálni az optimális utat a számkör fokozatos bővítésére. Pl. Szirmai tízesével bővíti a számkört, a gyakorlatból indul ki szöveges feladatokkal, majd elvégezteti az összes kapcsolódó számfeladatot, Beke egyre növekvő lépésekben bővíti a számkört, sorozatalkotás, számfeladatok, szöveges feladatok a sorrend. Az 1948-as Falusi [38.] és Városi [7.] tankönyvek szerzői mintha nem ismerték volna az 1. osztályos tankönyveket, ugyanis 2. osztályban tízes lépésenként, fokozatosan újra kezdik 100-ra bővíteni a számkört. Már mind a négy alapműveletet szétválasztják. Külön-külön fejezetben taglalják az összeadást, a kivonást, a pótlást, a szorzást, az osztást és a bennfoglalást is. A tananyag ilyetén strukturálásával visszatérnek a XVI‒XVIII. században bevett tananyag-feldolgozáshoz. Az 1951-es Budapesti tankönyv [8.] is ezt az utat választja. Az 1954-ben megjelent Nagy-tankönyvek [29.] újra törekednek visszaállítani a XX. század elején bevett gyakorlatot. Az 1963-tól 78-ig tartó időszakban a Csáki- [12.], Csáki–Géczy- [14.; 16.] tankönyvek, az 1947-es Budapesti tankönyv [8.] módszertani felépítését követik. Látszólag ez egyszerű másolás vagy visszalépés, de ha figyelembe vesszük a második tanév elejei előismereteket, mai szemmel inkább módszertani tévedésnek látszik. A 2010-es évek 2. osztályos könyvei közül ettől a gyakorlattól csak az Nemzeti Tankönyvkiadónál megjelent C. Neményi-tankönyvek [31.] és a Műszaki Könyvkiadó tankönyvei [23.] térnek el. Az első Csáki–Géczy-tankönyvben [14.] sorrendben, míg a másodikban [16.] már csoportosítva tanítják a szorzótáblákat. A szorzótáblák csoportosítása új metodikai eljárás. Azért lehetséges, mert teljesen szétválasztja a számkörbővítést a szorzótáblák tanításától, ami azt eredményezi, hogy a műveleti tulajdonságok megismertetésére külön ki kell térni. A szorzótáblák csoportosítása részben ezt a problémát hivatott áthidalni. A csoportosítással ugyanis adódik az egy-egy csoportba tartozó szorzótáblák közötti összefüggés megláttatása. A Csáki–Géczy [16.] gyakorlatát követi az Apáczai Kiadó [4–5.] és a Mozaik Kiadó [19.] tankönyve.
A feladatokban bekövetkezett változások
A feladatok vizsgálatát évfolyamonként egy kiválasztott témakör feladatszámának meghatározásával kezdtem, azonban részletgazdagabb képet kapok, ha a szám- és szövegesfeladat-típusokat külön-külön vizsgálom.
Változások a számfeladatokban
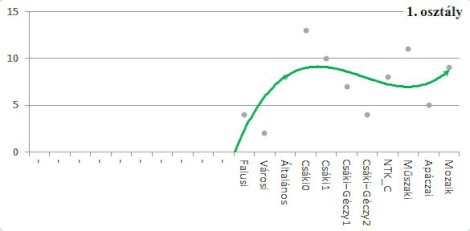
Az első osztályban az idő múlásával a feladatok száma erősen csökken, de a számfeladatok típusszámának trendvonala kicsiny mozgást mutat. A legtöbbféle feladatot a Csáki [11.] és a Műszaki [22.] tankönyv, a legkevesebb félét a Városi [32.] tankönyv tartalmazza.
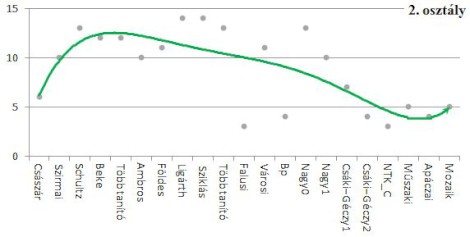
A második osztályban a 40-es számkörben, illetve a 4-es szorzótáblához kapcsolódó feladatok körében csökken a feladatok száma is, és a variabilitása is. Nagy különbség mutatkozik a XX. század első és második felében a számfeladatok típusai között. Ennek legszembetűnőbb oka a számkörbővítés stratégiájának megváltozása. Akkor voltak a legváltozatosabbak a vizsgált fejezetekben a számfeladatok, amikor a számfogalom és a műveletfogalom alakítása nem vált szét élesen, azaz egy-egy új számkör bevezetésével az adott számkörben mind a négy alapműveletet begyakorolták. A grafikonokon a szürke pontok az egy-egy tankönyv vizsgált fejezeteiben a számfeladatok típusszámát jelölik, a zöld görbe a polinomiális trendvonal.
Változások a szöveges feladatokban
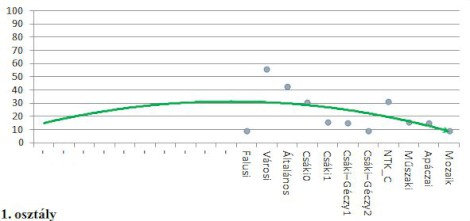
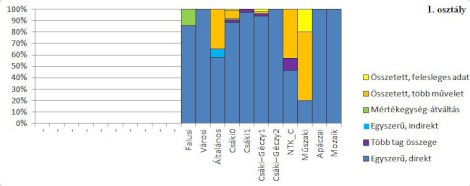
A szöveges feladatok százalékos arányának trendvonalát és a szöveges feladatok típusának százalékos előfordulását 1883–2010 között mutatják az alábbi grafikonok.
Az első osztályos tankönyvek vizsgált fejezeteiben 1948-tól egyre kisebb arányban fordulnak elő szöveges feladatok. A szöveges feladatok számának minimuma a mai Mozaik-tankönyvben [3.] mutatható ki. A szöveges feladatok típusát tekintve az idő múlásával a feladatok szövegei is egyszerűsödnek. Egyre több az egyszerű, direkt szövegezésű feladat, a Csáki–Géczy- [15.], az Apáczai- [20.] és a Mozaik- [3.] tankönyvek vizsgált fejezeteiben már csak ilyen típusú található. A mai tankönyvek közül kivételt képez a Nemzeti Tankönyvkiadónál megjelent C. Neményi-féle tankönyv [10.] és a Műszaki Könyvkiadó [22.] tankönyve, amelyekben nagy arányban szerepel összetett feladat, és a Műszaki-tankönyvben felesleges adatot tartalmazó feladat is van.
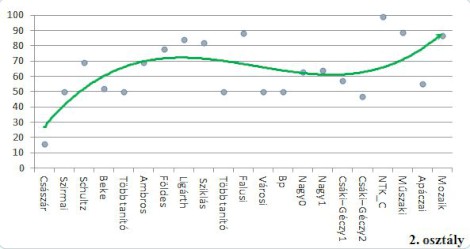
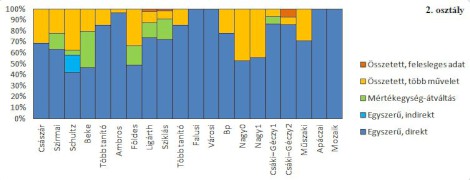
Második osztályban a XX. század második felében is csökken a szöveges feladatok aránya. A C. Neményi- [31.] és a Műszaki- [23.] tankönyvek meghaladják, a Mozaik- [4–5.] tankönyv eléri a XX. század első felének arányátlagát. Ugyanakkor az összetett, több művelettel megoldható feladatok aránya egyre kisebb.
A szakszavak használatában bekövetkezett változások
A szaknyelv létrejöttének célja az egzakt szakmai kommunikáció. A matematikai szaknyelv több szempontból is speciális a többi szaknyelvhez képest. Használata szélesebb körű, mint a legtöbb szaknyelvé, ugyanis több-kevesebb elemét más tudományterületek is átveszik, de a hétköznapi élet számos területén is szükséges a matematikai tartalmú kommunikáció. (Részletesen ír erről Czékmán Orsolya doktori értekezésében.) Ezért szervesen be kell épülnie az iskolai tananyagba is.
A matematikai szaknyelv sok szimbólumot, matematikai jelet tartalmaz, melyek részben kódok, részben fogalmak közötti relációt fejeznek ki. Ezek használatával egyszerűsödik a kommunikáció.
A vizsgálat ezen részében csak a betűvel leírt szavakat vettem számba, a szakszó megjelenését vizsgáltam, az előfordulás gyakoriságát nem.
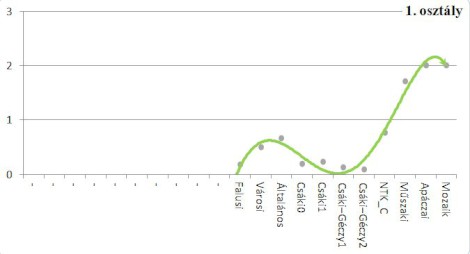
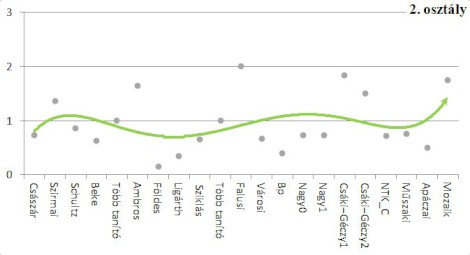
Az első osztályban 1962–78 között (a kísérleti könyvektől eltekintve) szinte eltűnnek a vizsgált fejezetből a szakszavak, az ezredforduló körül azután fokozatosan egyre nagyobb arányban jelennek meg. A második osztályban a kiválasztott témában az egyes tankönyvek nagyobb eltérés mutatnak, de a trendvonal kis hullámzással az oldalankénti 1 új szakszó körül mozog. Az alábbi grafikonok az egy oldalra jutó szakszavak számát és trendvonalát mutatják az 1. és 2. osztályos tankönyvekben.
Az illusztrációk megjelenésében, funkciójában bekövetkezett változások
Az illusztrációk fontos szerepet játszanak a tanultak megértésében és megjegyzésében. Wachsmuth szerint a matematikai gondolkodásban a bal agyféltekét működtetjük, amikor pl. a szisztematikus megoldásra, oksági gondolkodásra, rendezésére törekszünk. A jobb agyféltekét működtetjük, amikor pl. asszociációt végzünk, vagy párhuzamos gondolatmeneteket vetünk össze. Az információk megszerzése hatékonyabb, ha egyszerre több kommunikációs csatornát használunk, illetve tevékenységhez is kapcsolódik.1
A vizsgált időszakban a tankönyvi illusztrációk oldalankénti átlaga látványosan emelkedett, a nyomdatechnika fejlődésével a minősége is javult.
A matematikai tartalom és az illusztráció viszonyát 4 kategóriában vizsgáltam. Jól látható, hogy az irányított megfigyelést célzó ábrák egyre nagyobb arányban fordulnak elő. Kivétel az Apáczai-tankönyv [19.], ugyanis ebben a legnagyobb arányban a motiváló illusztráció fordul elő, amelyek nem segítik a matematikai gondolkodást.
Jelmagyarázat a grafikonokhoz
Kék: irányított megfigyelés
Piros: szemléltetésre támaszkodó magyarázat
Zöld: szemléleti igazolás
Sárga: motiváló illusztráció
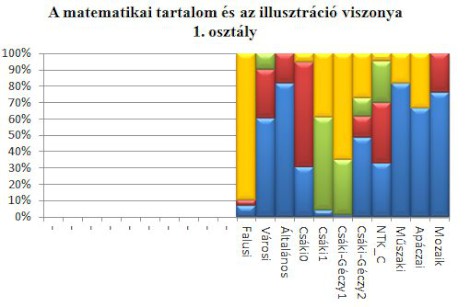
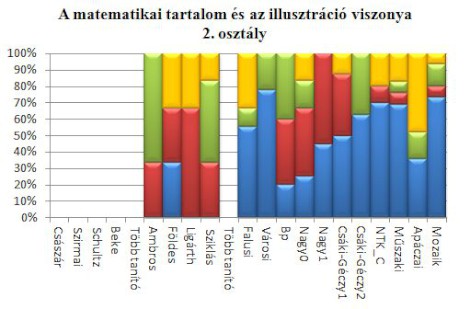
Az utóbbi évek 1-2. osztályos tankönyvek tananyagszerkesztése
Az utóbbi évek tankönyvei igen változatos formában közelítik meg a szám- és műveletfogalom tanítását, de mindegyik megközelítésre található már példa a XVIII‒XX. századi számtankönyvek valamelyikében. A 2. osztályos tankönyvek közel azonos 1. osztályos matematikai tartalomra építhetnek – összeadás, kivonás 20-as számkörben. A szorzótáblák tanításának elhelyezkedése a tananyagban három különféle tendenciát mutat, de látszik bizonyos törekvés a fogalomalakítás, begyakorlás minél hosszabb időbeli elhúzására. Ez, valamint a számolási készség fejlődési menete, a korai matematikai gondolkodás mentális modellje, nem utolsósorban a XX. század első felének tankönyvei indikálták a következő tananyag-szerkesztési koncepciót, amelyet az új kerettanterv lehetővé tesz azzal, hogy két tanévre határozza meg az elsajátítandó tananyagot, így a kétéves bontás egy-egy évfolyam esetén enged némi szabadságot.
A tankönyvkoncepció elveit az OFI szakemberei elfogadták, az intézet honlapján megjelentették, azonban a tankönyvkészítés során a koncepció alappilléreit kivették az alsó tagozatos tankönyvek felelősei. Ragaszkodnak az 50-es években kialakult feldolgozási modellhez, így jelenleg a megvalósításra csekély esély látszik.
Részletek egy tankönyvkoncepcióból
Az elmúlt 130 év tankönyveinek, módszertani útmutatóinak, tapasztalatainak figyelembevételével az 1–2. osztályos tananyag feldolgozását a következő tananyag-szerkesztési koncepcióban látom optimálisnak.
Az 1-2. osztályos koncepcióban a tananyagot a számkörbővítés köré csoportosítva építettem fel. A számkör lineárisan épül, az ehhez kapcsolódó fogalom- és tevékenységrendszert spirálisan. A számfogalom és a műveletfogalom alakítását – az összeadás-kivonás, az összeadás-szorzás, a szorzás-osztás különböző értelmezéseivel – párhuzamosan alakítom.2 A természetes szám megjelenik mint halmazok számossága, mint sorszám, mint különböző műveletek eredménye.
Nem elkülönítve, hanem minden számkörben megjelenik a kerettanterv által meghatározott öt fő egység. Több fő egység akár egy feladatban is megjelenhet. Igen korán elkezdődik a problémamegoldó gondolkodás fejlesztését. Ezeken belül kezdetben az ábrával adott feladatok, különböző „rejtvények”, majd a szám- és a szöveges feladatok kerülnek előtérbe. Kezdetben az egyszerű direkt és indirekt szövegezésű, majd az összetett, mértékeket tartalmazó, több művelettel megoldható, felesleges és hiányos adatokat tartalmazó, valamint az egyszerű realisztikus feladatok. A koncepcióból adódik, hogy a tárgyalásmód a matematikai fogalmak tartalmilag sokoldalú megközelítését, a feladatok sokféle megoldását, a kreativitás eredményes fejlesztését teszi lehetővé.
A számfogalom témakörben már a kezdeti időszakban sokrétűen beépülnek a geometria és mérés témakör feladatai. A tankönyv különböző feladattípusai mellett szükséges, hogy minden gyermek végezzen valóságos méréseket, dolgozzon a kézébe kapott síkidom-, illetve testmodellekkel. Modellezéssel, kivágással, színezéssel, építéssel oldjanak meg geometriai problémákat.
Az illusztrációk szorosan kapcsolódnak a matematikai tartalomhoz. Fontos szerepük van a tanultak megértésében és megjegyzésében, ezzel is fejlesztve az „információs híd”, a kérgestest (corpus callosum) célirányos működését.
A matematikai szaknyelvnek szervesen be kell épülniük az iskolai tananyagba is. A matematikai szaknyelv sok szimbólumot, jelet tartalmaz, melyek kódok vagy fogalmak közötti relációt fejeznek ki – ezek használatával egyszerűsödik a kommunikáció. Alapelvnek tekintem, hogy a matematikában általánossá vált szimbólumokat, valamint szakkifejezéseket a fogalmakkal együtt vezessük be, mivel tudjuk, hogy a megnevezés segíti a megértést és az alkalmazást. Nem kívánok olyan kifejezést, eljárást használni, amelyet később a matematikai tartalom bővülésével szükségszerű megváltoztatni.
A számjegyek, reláció- és műveleti jelek írástanításának menete a betűírás általánosan elfogadott menete alapján: kezdetben nagyobb, majd fokozatosan csökkenő rácsba íratva az első félév második harmadára jut el az 5 mm-es rácsban való íráshoz.
Feltehető a kérdés, hogy korunkban szükség van-e a kézírásra, fejszámolásra, amikor rendelkezésre állnak ezeket helyettesítő eszközök. A válasz igen, mivel ezen tevékenységek eredménye nem csupán a „végtermék”, a leírt szöveg vagy a kiszámolt eredmény. A fejszámolással fejlődnek pl. a gondolkodási műveletek (analízis, szintézis stb.), a módszerek, a modellben való gondolkodás is.
A jelenlegi számfogalom alakulását, fejlődését vizsgáló agykutatások alapján ma is érvényesnek tekinthetjük a XX. századra kialakult alapelvek alkalmazását: a szemléleten, a számok vizsgálatán, a számbeli viszonyok feldolgozásán alapuló számfogalom alakítását.
A hivatkozott tankönyvek listája
1. Ambros József – Kopeczky Ferenc, 1921. Számtani példatár az elemi népiskolák számára. II. füzet II. iskolaév hasonczímű műve után átdolgozta a csáktornyai községi elemi népiskolák tanítótestülete. 12. átdolgozott kiadás. Fischel, Nagykanizsa.
2. Apáczai Csere János, 1653. Magyar Encyclopaedia, azaz minden igaz és hasznos bölcsességnek szép rendbe foglalása és magyar nyelven világra bocsátása. Utrecht.
3. Árvainé Libor Ildikó – Lángné Juhász Szilvia – Szabados Anikó, 2009. Sokszínű matematika. Matematika 1. Munkatankönyv. Mozaik Kiadó, Szeged.
4. Árvainé Libor Ildikó – Lángné Juhász Szilvia – Szabados Ildikó, 2009. Sokszínű matematika. Matematika 2. Munkatankönyv I. félév. Mozaik Kiadó, Szeged.
5. Árvainé Libor Ildikó – Lángné Juhász Szilvia – Szabados Ildikó, 2009. Sokszínű matematika. Matematika 2. Munkatankönyv II. félév. Mozaik Kiadó, Szeged.
6. Beke Manó, 1903. Számtan a népiskolák II. osztályának. 3. kiadás. Magyar Királyi Tudományegyetemi Könyvnyomda, Budapest.
7. Bertalan Ferenc, 1947. Második könyvünk. Folyóírás, olvasmányok, nyelvi ismeretek, számolás és mérés. A városi iskolák számára. VKM, Budapest. 279–360.
8. Bertalan Ferenc, 1947. Második könyvünk. Folyóírás, olvasmányok, nyelvi ismeretek, számolás és mérés. Nagy-budapesti kötet. VKM, Budapest. 1–98.
9. Busse, F. G., 1786. Kleine Beyträge zur Mathematik und Physik und deren Lehrmethode Crusius, Lipcse.
10. C. Neményi Eszter – Sz. Oravecz Márta, 2009. Matematika 1. osztály. I., II. kötet. Nemzeti Tankönyvkiadó Zrt., Budapest.
11. Csáki Imre, 1954. Számtan az általános iskolák I. osztálya számára. Kísérleti tankönyv. Tankönyvkiadó, Budapest.
12. Csáki Imre, 1962. Számtan az általános iskolák I. osztálya számára. 7. kiadás. Tankönyvkiadó, Budapest.
13. Csáki Imre – Géczy Etelka, 1963. Számolás-mérés az általános iskolák I. osztálya számára. 14. kiadás. Tankönyvkiadó, Budapest.
14. Csáki Imre – Géczy Etelka 1963. Számolás-mérés az általános iskolák második osztálya számára. Tankönyvkiadó, Budapest.
15. Csáki Imre – Géczy Etelka, 1975. Számolás-mérés az általános iskolák 1. osztálya számára. Tankönyvkiadó, Budapest.
16. Csáki Imre – Géczy Etelka, 1976. Számolás-mérés az általános iskola 2. osztálya számára. 14. átdolgozott kiadás. Tankönyvkiadó, Budapest.
17. Császár Károly, 1883. Számvetés. A népiskolák 2. osztályában. Eggenberger-Fell Könyvkereskedés, Budapest.
18. (Ismeretlen szerző), 1577. Aritmetika azaz a számvetés tudománya, mell’ magyar nyelure (ez tudományban gyönyörködnec, hasznokra és hamarabb való értelmekre is móddal) forditatott. Azt akarom, hogy az io és hasznos dolgokban eszesek legyetek, az gonosz és ártalmas dolgokban pedig egiugiuek. Debreczen.
19. Esztergályos Jenő, 2009. Második matematikám. Az általános iskola 2. osztálya számára. Apáczai Kiadó, Celldömölk.
20. Esztergályos Jenő – Kuruczné Borbély Márta, 2009. Az én matematikám. Az általános iskola 1. osztálya számára. Apáczai Kiadó, Celldömölk.
21. Földes Károly, 1921. A számolás gyakorlókönyve. Az elemi népiskolák II. osztálya számára. Átdolgozta Bartha Pál. 3. kiadás. Lampel R. R.T., Budapest.
22. Hajdu Sándor – Novák Lászlóné – Scherlein Márta, 2009. Matematika 1. I–II. kötet. Műszaki Könyvkiadó, Budapest.
23. Hajdu Sándor – Novák Lászlóné – Scherlein Márta, 2009. Matematika 2. I–II. kötet. Műszaki Könyvkiadó, Budapest.
24. Ligárth Mihály 1930(?). Számtani és mértani példák gyűjteménye. Az elemi iskolák II. osztálya számára. Városi nyomda, Debrecen.
25. Maróthi György, 1734. Arithmetica vagy számvetésnek mestersége Mellyet írtt és Közönséges Haszonra, föképpen a’ Magyar országon elö fordúlható Dolgokra, alkalmaztatván ki-adott 1743-ik Esztendöben, Maróthi György, Debretzeni professor. Debretzen.
26. Maróthi György, 1782. Arithmetica vagy számvetésnek mestersége Debretzen.
27. Menyői Tolvaj Ferenc, 1735. Az arithmetikanak, avagy az számlálásnak oet speciesinek rövid magyar regulakban foglaltatott mestersege. Brassó.
28. Nagy Károly, 1837. A kis számító. Magyar gyermekek kézikönyve. Hohrmann‒Schweigerd, Bécs.
29. Nagy László, 1954. Számtan az általános iskolák II. osztálya számára. Kísérleti könyv. Tankönyvkiadó, Budapest.
30. Nagy László, 1962. Számtan az általános iskolák II. osztálya számára. 7. kiadás. Tankönyvkiadó, Budapest.
31. Neményi Eszter, C. – Oravecz Márta, Sz., 2009. Matematika általános iskola 2. osztály. I‒II. kötet Nemzeti Tankönyvkiadó Zrt., Budapest.
32. Oldal Anna, 1948. Első könyvünk. Alapírás, olvasmányok, számolás és mérés. A városi iskolák számára. VKM, Budapest. 175–231.
33. Oldal Anna – Makoldi Mihályné – Varga Tamás, 1951. Első könyvünk. Az általános iskolák számára. Tankönyvkiadó, Budapest. 181–264.
34. Onadi János, 1693. Practici Algorithmi Erotemata Methodica. Kassa.
35. Schultz Imre, 1899. Leányiskolai számolókönyv 4 részben. 1. rész. A második osztály számára. Stampfel Károly, Pozsony.
36. Sziklás Adolf – Walter Károly, 1925(?). Számtani példatár. Az elemi népiskolák II. osztálya számára. Lampel R. R. T., Budapest.
37. Szirmai József 1893. Népiskolai számoló-könyv. Koronaérték szerint, 1. füzet: A második osztály számára. Franklin-Társulat, Budapest.
38. Tóth Mihály, 1948. Második könyvünk. Folyóírás, olvasmányok, nyelvi ismeretek, számolás és mérés. A falusi iskolák számára. VKM, Budapest, 247–351.
39. Több fő- és székvárosi tanító, 1904. Számolókönyv. Az elemi népiskolák 2. osztálya számára. Franklin Társulat, Budapest.
40. Több fő- és székvárosi tanító, 1906. Számolókönyv. Az elemi népiskolák II. osztálya számára. Franklin Társulat, Budapest.
A téma részletes kifejtését lásd a szerző doktori disszertációjában.
- 1. Wachsmuth, I. (1981): Two Models of Thinking – Also Relevant for the Learning of Mathematics. In: For the Learning of Mathematics 2 (2) 38-45.
- 2. Egyszerű problémákban már a 6-os számnál megjelenik a szorzás-osztás fogalma, kapcsolata egymással, valamint az összeadással, kivonással is. Innentől kezdve minden egyes számkörben tapasztalatot szereznek a tanulók nemcsak a számkörben elvégezhető összeadás-kivonásról, hanem a szorzás-osztásról is. Ebben a periódusban a szorzatok, hányadosok magához a számhoz kapcsolódnak. Például a 12-es számkörben a feladatokban megjelenik az 1×12, 12×1, 2×3, 6×2, 3×4, 4×3; 12:2-vel, 3-mal stb. is. A szorzótábla (szorzás, osztás, bennfoglalás, maradékos osztás) szisztematikus felépítése a 2. osztályba kerül. Így a 2-es szorzótábla már az év elején az ismétlő periódusban megjelenik. A 0-30-ig számolunk részben a 3-as szorzótábla és a hozzá kapcsolódó ismeretanyag jelenik meg, a 30-as számkörben elvégezhető összes alapművelettel.
